FaCiLe offers variables and constraints on integer and set finite
domains. This chapter first describes how to build a constraint
program on standard integer variables, while explaining the basics
underlying concepts of FaCiLe. Then section 2.7 extends
the scheme to set variables, which work in a similar fashion.
2.1 Domains
Finite domains of integers are created, accessed and handled with
functions of module Domain (exhaustively described in section
??). Domains basically are sets of "elements" of
type Domain.elt (here integers, or sets of integers for the set
domains described in section 2.7.1). They are represented
as functional objects of (abstract)
type Domain.t and can therefore be shared. Domains are built with
different functions according to the domain properties:
-
Domain.empty is the empty domain;
Domain.create is the most general constructor and builds a domain from a
list of integers, possibly unsorted and with duplicates;
Domain.interval is a shorthand when domains are continuous;
Domain.boolean is a shorthand for create [0;1];
Domain.int is the largest (well, at least very large) domain.
Domains can be conveniently printed on an output channel with
Domain.fprint and are displayed as lists of non-overlapping intervals and
single integers
[inf1-sup1;val2;inf3-sup3;...] in increasing order:
let discontinuous = Domain.create [4;7;2;4;-1;3];;
val discontinuous : Facile.Domain.t = <abstr>
Domain.fprint stdout discontinuous;;
[-1;2-4;7]- : unit = ()
let range = Domain.interval 4 12;;
val range : Facile.Domain.t = <abstr>
Domain.fprint stdout range;;
[4-12]- : unit = ()
Various functions allow access to properties of domains like, among
others (see ??), Domain.is_empty, Domain.min,
Domain.max whose names are self-explanatory:
Domain.is_empty range;;
- : bool = false
Domain.max range;;
- : Facile.Domain.elt = 12
Domain.member 3 discontinuous;;
- : bool = true
Domain.values range;;
- : Facile.Domain.elt list = [4; 5; 6; 7; 8; 9; 10; 11; 12]
Operators are provided as well to handle domains and easily perform
set operations like Domain.intersection, Domain.union,
Domain.difference and domain reduction like Domain.remove,
Domain.remove_up, Domain.remove_low, etc. (see ??):
Domain.fprint stdout (Domain.intersection discontinuous range);;
[4;7]- : unit = ()
Domain.fprint stdout (Domain.union discontinuous range);;
[-1;2-12]- : unit = ()
Domain.fprint stdout (Domain.remove_up 3 discontinuous);;
[-1;2-3]- : unit = ()
Domain.fprint stdout (Domain.remove_closed_inter 7 10 range);;
[4-6;11-12]- : unit = ()
2.2 Variables
FaCiLe variables are attributed objects[6] which
maintain their current domain and can be backtracked during the execution of search
goals.
Creation
FaCiLe finite domain constrained variables are build and handled by
functions of module Var.Fd (described exhaustively in section
??). Variables are objects of type Fd.t
created by a call to one of the following functions of module Var.Fd:
-
create d takes a domain d as argument.
interval inf sup yields a variable whose domain ranges the
interval [inf..sup]. It is equivalent to
create (Domain.interval inf sup).
array n inf sup creates an array of n ``interval''
variables. Equivalent to Array.init n
(fun _ -> Fd.interval inf sup).
int n returns a variable already bound to n.
Note that the submodule Fd can be reached by opening module
Easy; in all the toplevel examples, modules Facile and
Easy are supposed open, therefore a function f of module
Fd is called with Fd.f instead of
Facile.Var.Fd.f.
The first three creation functions actually have an optional argument
labelled ?name which allows to associate a string identifier to
a variable. The ubiquitous fprint function writes a variable
on an output channel and uses this string name if provided or an
internal identifier if not:
let vd = Fd.create name:"vd" discontinuous;;
val vd : Facile.Var.Fd.t = <abstr>
Fd.fprint stdout vd;;
vd[-1;2-4;7]- : unit = ()
Attribute
A FaCiLe variable can be regarded as either in one of the following two
states:
-
uninstantiated or unbound, such that an ``attribute''
containing the current domain (of size strictly greater than one) is
attached to the variable;
- instantiated or bound, such that merely an integer
is attached to the variable.
So an unbound variable is associated with an attribute of type
Var.Attr.t holding its current domain, its string name, a unique integer
identifier and various internal data irrelevant to the end-user. Functions to
access attributes data are gathered in module Var.Attr:
-
dom returns the current domain of an attribute;
- the mapping of
fprint, min, max, size,
member of module Domain applied on the embedded domain of
an attribute (e.g. min a is equivalent to Domain.min (dom a));
id to get the identifier of an attribute;
constraints_number returns the number of ``active'' constraints
still attached to a variable.
Although variables are of abstract type Fd.t, function
Fd.value v returns a concrete view of type
Var.concrete_fd = Unk of Attr.t | Val of int
1
of a variable v, so that a control structure that depends on the
instantiation of a variable will typically look like:
match Fd.value v with
Val n -> f_bound n
| Unk attr -> f_unbound attr
An alternative boolean function Fd.is_var returns the current state
of a variable, sparing the ``match'' construct.
let v1 = Fd.create (Domain.create [1]) (* equivalent to Fd.int 1 *);;
val v1 : Facile.Var.Fd.t = <abstr>
Fd.is_var v1;;
- : bool = false
Fd.fprint stdout v1;;
1- : unit = ()
Domain Reduction
Module Fd provides two functions to perform
backtrackable domain reductions on variables, typically used within
instantiation goals and filtering of user-defined constraints:
Fd.fprint stdout vd;;
vd[-1;2-4;7]- : unit = ()
match Fd.value vd with
Val n -> () (* Do nothing *)
| Unk attr -> (* Remove every value > 2 *)
let new_dom = Domain.remove_up 2 (Var.Attr.dom attr) in
Fd.refine vd new_dom;;
- : unit = ()
Fd.fprint stdout vd;;
vd[-1;2]- : unit = ()
Whenever the domain of a variable becomes empty, a failure occurs (see
2.5 for more explanations about failure):
match Fd.value vd with
Val n -> () (* Do nothing *)
| Unk attr -> (* Remove every value < 4 *)
let new_dom = Domain.remove_low 4 (Var.Attr.dom attr) in
Fd.refine vd new_dom;;
Exception: Fcl_stak.Fail "Var.XxxFd.refine".
Access
Besides Fd.value and Fd.is_var which access the state of
a variable, module Fd provides the mapping of module Domain
functions like Fd.size, Fd.min, Fd.max, Fd.values,
Fd.iter and Fd.member, and they return meaningful values whatever
the state (bound or unbound) of the variable may be:
let vr = Fd.interval 5 8;;
val vr : Facile.Var.Fd.t = <abstr>
Fd.size vr;;
- : int = 4
let v12 = Fd.int 12;;
val v12 : Facile.Var.Fd.t = <abstr>
Fd.member v12 12;;
- : bool = true
Contrarily, function Fd.id, which returns the unique identifier associated
with a variable, or function Fd.name, which returns its specified string
name, only work if the variable is still uninstantiated, otherwise an exception is
raised.
An order based on the integer identifiers is defined by function
Fd.compare2 as well as an equality function Fd.equal, observing
the following two rules:
-
bound variables are smaller than unbound variables;
- unbound variables are compared according to their identifiers.
Fd.id vr;;
- : int = 2
Fd.id v12;;
Exception: Failure "Fatal error: Var.XxxFd.id: bound variable".
Fd.compare v12 (Fd.int 11);;
- : int = 1
Fd.compare vr v12;;
- : int = 1
Fd.id vd;;
- : int = 0
Fd.compare vd vr;;
- : int = -1
Eventually, function Fd.elt_value returns the integer value of a
bound variable. If the variable is not instantiated, an exception is raised.
Fd.elt_value (Fd.int 1);;
- : Facile.Var.Fd.elt = 1
Fd.elt_value (Fd.interval 0 1);;
Exception: Failure "Fatal error: Var.XxxFd.elt_value: unbound variable: _3".
2.3 Arithmetic Expressions
Arithmetic expressions and constraints over finite domain variables
are built with functions and operators of module Arith (see
??).
Creation and Access
Arithmetic expressions are objects of abstract type Arith.t which
contain a representation of an arithmetic term over finite domain variables.
An expression is ground when all the variables used to build it
are bound; in such a state an expression can be ``evaluated'' with
function Arith.eval which returns its unique integral value.
A call to Arith.eval with an expression that is not ground raises
the exception Invalid_argument. However, any expression can be printed
on an output channel with function Arith.fprint.
A variable of type Fd.t or an OCaml integer of type int
are not arithmetic expressions and therefore cannot be mixed up
with the latter. ``Conversion'' functions are provided by module
Arith to build an expression from variables and integers:
-
Arith.i2e n returns an expression which evaluates to
integer n;
Arith.fd2e v returns an expression which evaluates to n
when v is bound to n.
Handily enough, opening module Easy allows direct access to
most useful functions and operators of module Arith, including
i2e and fd2e:
let v1 = Fd.interval 2 5;;
val v1 : Facile.Var.Fd.t = <abstr>
let exp1 = fd2e v1;;
val exp1 : Facile.Arith.t = <abstr>
Arith.fprint stdout exp1;;
_4[2-5]- : unit = ()
Arith.eval exp1;;
Exception: Failure "Fatal error: Expr.eval: variable _4 unknown".
Fd.unify v1 4;;
- : unit = ()
Arith.eval exp1;;
- : int = 4
Arith.fprint stdout (i2e 2);;
2- : unit = ()
Maximal and minimal values of expressions can be accessed by functions
Arith.max_of_expr and Arith.min_of_expr:
let exp2 = fd2e (Fd.interval (-3) 12);;
val exp2 : Facile.Arith.t = <abstr>
Arith.min_of_expr exp2;;
- : int = -3
Arith.max_of_expr exp2;;
- : int = 12
Conversely, an arithmetic expression can be transformed into a variable thanks
to function Arith.e2fd which creates a new variable constrained
to be equal to its argument (see 2.4.2).
Operators
Module Arith provides classic linear and non-linear arithmetic
operators to build complex expressions. Most frequently used ones can
be directly accessed through the opening of module Easy, which
considerably ligthen the writing of equations, especially for binary
infix operators.
-
+~, -~, *~, /~: addition, substraction,
multiplication and division (the exception
Division_by_zero is raised whenever its second argument evaluates to 0).
e **~ n raises e to the nth power, where n is an
integer.
x %~ y: modulo. The exception Division_by_zero is raised
whenever y evaluates to 0.
Arith.abs: absolute value.
let vx = Fd.interval name:"x" 3 6 and vy = Fd.interval name:"y" 4 12;;
let exp1 = i2e 2 * fd2e vx - fd2e vy + i2e 3;;
val exp1 : Facile.Arith.t = <abstr>
Arith.fprint stdout exp1;;
3 + -y[4-12] + 2 * x[3-6]- : unit = ()
Arith.min_of_expr exp1;;
- : int = -3
Arith.max_of_expr exp1;;
- : int = 11
Global arithmetic operators working on array of expressions are provided
as well:
-
Arith.sum exps builds the sum of all the elements of
the array of expressions exps.
Arith.scalprod ints exps builds the scalar products of
an array of integers by an array of expressions. Arith.scalprod
raises Invalid_argument if the two arrays have not the same
length.
Arith.prod exps builds the product of all the elements of
the array of expressions exps.
Their variable counterparts where the array of expressions is replaced by
an array of variables are defined as well: Arith.sum_fd,
Arith.scalprod_fd, Arith.prod_fd. Note that Arith.sum_fd a,
for example, is simply defined as Arith.sum (Array.map fd2e a).
let size = 5;;
val size : int = 5
let coefs = Array.init size (fun i -> i+1);;
val coefs : int array = [|1; 2; 3; 4; 5|]
let vars = Fd.array size 0 9;;
val vars : Facile.Var.Fd.t array =
[|<abstr>; <abstr>; <abstr>; <abstr>; <abstr>|]
let pscal_exp = Arith.scalprod_fd coefs vars;;
val pscal_exp : Facile.Arith.t = <abstr>
Arith.fprint stdout pscal_exp;;
1 * _8[0-9] + 2 * _9[0-9] + 3 * _10[0-9] + 4 * _11[0-9] + 5 * _12[0-9]- : unit =
()
Arith.min_of_expr pscal_exp;;
- : int = 0
Arith.max_of_expr pscal_exp;;
- : int = 135
2.4 Constraints
2.4.1 Creation and Use
A constraint in FaCiLe is a value of type Cstr.t. It can be
created by a built-in function (arithmetic, global constraints) or
user-defined (see 3.3). A constraint must be posted
with the function Cstr.post to be taken into account,
i.e. added to the constraint store. The state of the system can
then be accessed by a call to the function Cstr.active_store
which returns the list of all constraints still ``unsolved'', i.e. not
yet globally consistent.
When a constraint is posted, it is attached to the involved variables
and activated: propagation occurs as soon as the constraint is
posted. Consequently, if an inconsistency is detected prior to the
search, i.e. before the call to Goals.solve (see 2.5), a
Stak.Fail exception is raised. However, inconsistencies
generally occur during the search so that failures are caught by the
goal solving mechanism of FaCiLe which will backtrack until the
last choice-point.
Constraints basically perform domain reductions on their involved
variables, first when posted and then each time that a particular
``event'' occurs on their variables. An event corresponds to a domain
reduction on a variable: the minimal or maximal value has changed, the
size of the domain has decreased or the variable has been bound. All
these kinds reduction cause different events to trigger the
``awakening'' of the appropriate constraints. See 3.2.1 for a
more precise description of this event-driven mechanism.
Constraints can also be printed on an output channel with function
Cstr.fprint which usually yields useful information about
the variables involved and/or the name of the constraint.
2.4.2 Arithmetic Constraints
The simplest and standard constraints are relations on arithmetic
expressions (c.f. 2.3):
-
equality
=~
- strict and non-strict inequality
<~, >~, <=~,
>=~
- disequality
<>~
FaCiLe provides them as infix operators
suffixed with the ~ character, similarly to expression operators. These
operators are declared in the Easy module and don't need
module prefix notation whenever Easy is opened. The small example
below uses the equality operator =~ and points out the effect on
the variables domains of posting the constraint equation:
(* 0<=x<=10, 0<=y<=10, 0<=z<=10 *)
let x = Fd.interval 0 10 and y = Fd.interval 0 10 and z = Fd.interval 0 10;;
let equation = (* x*y - 2*z >= 90 *)
fd2e x * fd2e y - i2e 2 * fd2e z >= i2e 90;;
val equation : Facile.Cstr.t = <abstr>
(* before propagation has occurred *)
Cstr.fprint stdout equation;;
3: +2._15[0-10] -1._16[0-100] <= -90- : unit = ()
Cstr.post equation;;
- : unit = ()
(* after propagation has occurred *)
Cstr.fprint stdout equation;;
3: +2._15[0-5] -1._16[90-100] <= -90- : unit = ()
Notice that the output of the Cstr.fprint function does not
look exactly like the stated inequation but gives a hint about how the
two operands of the main sum are internally reduced into new single
variables constrained to be equal to the latters. This mechanism is of
course hidden to the user and is only unfolded when using the
pretty-printer.
FaCiLe compiles and simplifies (``normalizes'') arithmetic constraints
as much as possible so that variables and integers may be scattered inside
an expression with no loss of efficiency. Therefore the constraint
ineq1:
let x = Fd.interval (-2) 6 and y = Fd.interval 4 12;;
let xe = fd2e x and ye = fd2e y;;
let ineq1 = i2e 3 * ye + i2e 2 * xe * ye * i2e 5 * xe + ye >= i2e 4300;;
val ineq1 : Facile.Cstr.t = <abstr>
Cstr.fprint stdout ineq1;;
6: -4._18[4-12] -10._20[0-432] <= -4300- : unit = ()
which ensures 3y+(2xy×5x)+y ³ 4300, i.e. 10x2y+4y ³ 4300,
is equivalent to ineq2:
let ineq2 = i2e 10 * (xe ** 2) * ye + i2e 4 * ye >= i2e 4300;;
val ineq2 : Facile.Cstr.t = <abstr>
Cstr.fprint stdout ineq2;;
9: -4._18[4-12] -10._22[0-432] <= -4300- : unit = ()
Once posted, ineq1 or ineq2 incidentally yield a single
solution:
Printf.printf "x= x=_17[-2-6] y=_18[4-12]
- : unit = ()
Cstr.post ineq1;;
- : unit = ()
Printf.printf "x= x=6 y=12
- : unit = ()
It is also worth mentioning that arithmetic constraints involving
(large enough) sums of boolean variables are automatically detected
by FaCiLe and handled internally by a specific efficient mechanism.
The user may thus be willing to benefit from these features by
choosing a suitable problem modeling. This automatic behaviour can
be tuned by specifying the minimum size from which the constraint
is optimized (see ??).
Note on Overflows
Users should be carefull when expecting the arithmetic solver to
compute bounds from variables with very large domain, that means with
values close to max_int or min_int (depending on the
system and architecture). Especially with exponentiation and
multiplication, an integer overflow may occur which will yield an
error message ("Fatal error: integer overflow") on stderr and
an exception (Assert_failure) if the program is compiled in
byte code. A spurious calculation (probably leading to a failure
during propagation) will happen if it is compiled in native code. An
unexpected behaviour when performing such operations in native code
should thus always be checked against the safer byte code version.
2.4.3 Global Constraints
Beside arithmetic constraints, FaCiLe provides so-called ``global
constraints'' which express a relation on a set of variables. They are
defined in separate modules in which a function (and possibly several
variants) usually named cstr yields the constraint; these
functions takes an array of variables as their main argument.
The most famous one is probably the ``all different'' constraint which
expresses that all the elements of an array of variables must take
different values. This constraint is invoked by the function
Alldiff.cstr ?algo vars where vars is an array of
variables and ?algo an optional argument (of type Alldiff.algo)
that controls the efficiency of the constraint (see ??):
-
Lazy waits for the instantiation of a variable and
then removes the chosen value from the domains of the remaining variables;
Bin_matching evt uses a more sophisticated algorithm
(namely a ``bin matching'' [5]) which is called whenever
the event evt (see 3.2.1) occurs on one of the variables
to globally check the satisfiability of the constraint.
let vars = Fd.array 5 0 4;;
val vars : Facile.Var.Fd.t array =
[|<abstr>; <abstr>; <abstr>; <abstr>; <abstr>|]
let ct = Alldiff.cstr vars;;
val ct : Facile.Cstr.t = <abstr>
Fd.fprint_array stdout vars;;
[|_23[0-4]; _24[0-4]; _25[0-4]; _26[0-4]; _27[0-4]|]- : unit = ()
Cstr.post ct; Fd.unify vars.(0) 3;;
- : unit = ()
Fd.fprint_array stdout vars;;
[|3; _24[0-2;4]; _25[0-2;4]; _26[0-2;4]; _27[0-2;4]|]- : unit = ()
Module FdArray provides the ``element'' constraint named
FdArray.get which allows to index an array of variables by a variable,
and the min (resp. max) constraint which returns a variable
constrained to be equal to the variable that will instantiate to the minimal
(resp. maximal) value among the variables of an array:
let vars = [|Fd.interval 7 12; Fd.interval 2 5; Fd.interval 4 8|];;
val vars : Facile.Var.Fd.t array = [|<abstr>; <abstr>; <abstr>|]
let index = Fd.interval (-10) 10;;
val index : Facile.Var.Fd.t = <abstr>
let vars_index = FdArray.get vars index;;
val vars_index : Facile.Var.Fd.t = <abstr>
Fd.fprint stdout index;;
_31[0-2]- : unit = ()
Fd.fprint stdout vars_index;;
_32[2-12]- : unit = ()
let mini = FdArray.min vars;;
val mini : Facile.Var.Fd.t = <abstr>
Fd.fprint stdout mini;;
_33[2-5]- : unit = ()
FdArray.get and FdArray.min, which produce a new variable
(and thus hide an underlying constraint), also have their
``constraint'' counterpart FdArray.get_cstr and
FdArray.min_cstr which take an extra variable as argument and
return a constraint of type Cstr.t that must be posted to be
effective: FdArray.min_cstr vars mini is therefore equivalent
to the constraint:
fd2e (FdArray.min vars) =~ fd2e mini,
and
FdArray.get_cstr vars index v to:
fd2e (FdArray.get vars index) =~ fd2e v.
More sophisticated global constraints are available as well as FaCiLe
built-in constraints:
-
the global cardinality constraint [9]
(a.k.a. ``distribute'' constraint):
Gcc.cstr (see ??);
- the sorting constraint [3]:
Sorting.cstr
(see ??).
2.4.4 Reification
FaCiLe constraints can be ``reified'' thanks to the Reify module
and its function Reify.boolean (see ??) which takes
an argument of type Cstr.t and returns a new boolean variable.
This boolean variable is interpreted as the truth value of the relation
expressed by the constraint and the following equivalences hold:
-
the boolean variable is bound to 1 iff the constraint is satisfied,
and the constraint is thereafter posted;
- the boolean variable is bound to 0 iff the constraint is violated,
and the negation of the constraint is thereafter posted;
otherwise, i.e. it is not yet known if the constraint is satisfied or
violated and the boolean variable is not instantiated, the reification
of a constraint does not perform any domain reduction on the variables
involved.
In the following example, the boolean variable x_less_than_y
is constrained to the truth value of the inequation constraint x < y:
let x = Fd.interval 3 6 and y = Fd.interval 5 8;;
val x : Facile.Var.Fd.t = <abstr>
val y : Facile.Var.Fd.t = <abstr>
let x_less_than_y = Reify.boolean (fd2e x < fd2e y);;
val x_less_than_y : Facile.Var.Fd.t = <abstr>
Fd.fprint stdout x_less_than_y;;
_36[0-1]- : unit = ()
Cstr.post (fd2e y >= i2e 7);;
- : unit = ()
Fd.fprint stdout x_less_than_y;;
1- : unit = ()
Fd.fprint stdout (Reify.boolean (fd2e x = fd2e y));;
0- : unit = ()
When posted, the reification of a constraint calls the check function
(see 3.3) of the constraint, which verifies
whether it is satisfied or violated (without performing domain reduction).
If it is violated, the negation of the constraint is posted with a call
to another function of the constraint dedicated to reification,
namely not (see 3.3). Both functions are always defined
for all constraints but their default behaviour is merely exception
raising (Failure "Fatal error: ...") which means that the constraint
is actually not reifiable - as specified in the documentation of the
relevant constraints in the reference manual.
Roughly, arithmetic constraints are reifiable (as well as the ``interval''
constraint of module Interval, see ??) while
others (global ones) are not.
Reified constraint are by default woken up with the events triggering
its standard awakening (i.e. as if it were directly posted) and those of
its negation. This behaviour might possibly be too time costly (for
some specific problem) and the call to
Reify.boolean with its optional argument
?delay_on_negation (see ??) set to false
disables it, i.e. the events associated with the negation of the
constraint are ignored.
Module Reify also provides standard logical (most of them infix)
operators over constraints:
-
&&~~, conjunction;
||~~, disjunction;
=>~~, implication;
<=>~~, equivalence;
xor3, exclusive or;
not2.4.4, negation.
These operators can be directly accessed through the opening of module
Easy, except Reify.not (for obvious reasons) and
Reify.xor (which are not infix). Note that, unlike
Reify.boolean, these operators do not have a ?delay_on_negation
optional argument, so that the constraints they return will be woken
by both the events of their arguments and those of the negations of their
arguments.
These operators can be combined to yield complex logical
operators. For example, the ``exclusive or'' may be redefined in the
following way:
let x = Fd.interval 3 5 and y = Fd.interval 5 7;;
val x : Facile.Var.Fd.t = <abstr>
val y : Facile.Var.Fd.t = <abstr>
let xor ct1 ct2 = Reify.not (ct1 <=> ct2) in
let xor_cstr = xor (fd2e x = i2e 5) (fd2e y = i2e 5) in
Cstr.post (xor_cstr);
Cstr.post (fd2e x <= i2e 4);
Printf.printf "x= x=_38[3-4] y=5
- : unit = ()
Furthermore, module Arith contains convenient shortcuts to reify
its basic arithmetic constraints:
=~~, <>~~, <=~~, >=~~, <~~, >~~
These operators stand for the reification (and transformation into
arithmetic expression) of their basic counterparts, i.e. they take
two arithmetic expressions as operands and yield a new arithmetic
expression being the boolean variable related to the truth value of the
arithmetic constraint. e1 =~~ e2 is therefore equivalent to
fd2e (Reify.boolean (e1 =~ e2))
These operators can also be directly accessed through the opening of module
Easy. In the following example, the constraint stating that at least
two of the three variables contained in array vs must be
greater than 5 is expressed with the reified greater or equal
>=~~:
let vs = Fd.array 3 0 10;;
val vs : Facile.Var.Fd.t array = [|<abstr>; <abstr>; <abstr>|]
Cstr.post (Arith.sum (Array.map (fun v -> fd2e v > i2e 5) vs) >= i2e 2);
Fd.fprint_array stdout vs;;
[|_40[0-10]; _41[0-10]; _42[0-10]|]- : unit = ()
If vs.(1) is forced to be less than 5, the two other variables become
greater than 5:
Cstr.post (fd2e vs.(1) <= i2e 5);
Fd.fprint_array stdout vs;;
[|_40[6-10]; _41[0-5]; _42[6-10]|]- : unit = ()
2.5 Search
Most constraint models are not tight enough to yield directly a single
solution, so that search (and/or optimization) is necessary to find
appropriate ones. FaCiLe uses goals to search for solutions.
All built-in goals and functions to create and combine goals are
gathered in module Goals (see ??). This section
only introduces ``ready-to-use'' goals intended to implement basic
search strategies, but more experienced users shall refer to sections
3.1.2 and 3.4, where combining goals
with iterators and building goals from scratch are explained.
FaCiLe's most standard labeling goals is Goals.indomain which
instantiates non-deterministically a single variable by disjunctively
trying each value still in its domain in increasing order. To be
executed, a goal must then be passed as argument to function
Goals.solve which returns true if the goal succeeds or
false if it fails.
let x = Fd.create (Domain.create [-4;2;12]);;
val x : Facile.Var.Fd.t = <abstr>
Goals.solve (Goals.indomain x);;
- : bool = true
Fd.fprint stdout x;;
-4- : unit = ()
So the first attempt to instantiate x (to -4) obviously succeeds.
The values of the domain of x can be enumerated with a slightly
more sophisticated goal which fails just after Goals.indomain.
Module Goals provides Goals.fail, which is a goal that
always fails, and conjunction and disjunction operators,
respectively &&~ and ||~ (which can be directly accessed
when module Easy is open), to combine simple goals.
Hence such an enumeration goal would look like:
Goals.indomain x &&~ Goals.fail
But the result of such a goal will be a failure and the state of the
system (variable x not instantiated) will not be restored. A
simple disjunction of this goal with the goal that always succeeds,
Goals.success, yields the desirable behaviour:
(Goals.indomain x &&~ Goals.fail) ||~ Goals.success
In order to display the execution of this goal, a printing goal
gprint_fd which prints a variable on the standard
output (but will not be detailed in this section, see 3.4.1)
can eventually be inserted (conjunctively) between indomain
and fail:
let x = Fd.create (Domain.create [-4;2;12]);;
val x : Facile.Var.Fd.t = <abstr>
let goal = (Goals.indomain x gprint_fd x Goals.fail) || Goals.success;;
val goal : Facile.Goals.t = <abstr>
Goals.solve goal;;
-4 2 12 - : bool = true
Note that, unfortunately, the logical operators do have the same
priority. Hence goals expressions must be carefully parenthesized to
produce the expected result.
Module Goals also provides the function Goals.instantiate
that allows to specify the ordering strategy of the labeling.
Goals.instantiate takes as first argument a function to which is given
the current domain of the variable (as single argument) and should return
an integer candidate for instantiation. Labeling of variable x in
decreasing order is then merely:
let label_and_print labeling v =
(labeling v gprint_fd v Goals.fail) || Goals.success;;
val label_and_print :
(Facile.Var.Fd.t -> Facile.Goals.t) -> Facile.Var.Fd.t -> Facile.Goals.t =
<fun>
Goals.solve (label_and_print (Goals.instantiate Domain.max) x);;
12 2 -4 - : bool = true
Function label_and_print is defined here to lighten the
writing of enumeration goals (it takes only the instantiation goal
and the variable as arguments). In the example below, variable
x is labelled in increasing order of the absolute value of its
values. Function Domain.choose allows to only specify the
relevant order:
let goal =
label_and_print
(Goals.instantiate (Domain.choose (fun v1 v2 -> abs v1 < abs v2))) x;;
val goal : Facile.Goals.t = <abstr>
Goals.solve goal;;
2 -4 12 - : bool = true
Beside non-deterministic instantiation, FaCiLe provides also
Goals.unify to enforce the instantiation of a variable (which
might be already bound) to a given integer value:
Goals.solve (Goals.unify x 2);;
- : bool = true
Fd.fprint stdout x;;
2- : unit = ()
Goals.solve (Goals.unify x 12);;
- : bool = false
Goals.solve (Goals.unify (Fd.int 0) 0);;
- : bool = true
Search strategy
Like most CP system, FaCiLe default standard strategy is Depth First
Search. However, FaCiLe now offers Limited Discrepancy
Search [4] as well (see ??), and even
if a general mechanism to change the search strategy is not provided,
skilled users are encouraged to plunder and hack the source code of
module Goals to devise new custom strategies themselves.
Floundering
If the search goal does not instantiate all the variables involved in
the posted constraints, some of the constraints may still be unsolved
when a solution is found, so that this solution may be incorrect.
To be sure that all the constraints have been solved, the user can use
the function Cstr.active_store and checks that the returned
constraints list is empty. This checking may be done after the completion
of the search, i.e. after Goals.solve, or better, embedded within
the search goal. The latter allows to cleanly integrate this verification
in optimization and ``findall'' goals. A ``non-floundering check'' goal
could be implemented in the following way (function Goals.atomic
used here to build a new atomic goal is explained in section 3.4.1):
let check_floundering =
Goals.atomic
(fun () ->
if Cstr.active_store () <> [] then
failwith "Some constraints are still unsolved");;
val check_floundering : Facile.Goals.t = <abstr>
A simple conjunction with check_floundering at the end of the labeling
goal will do the job. Information about the alive constraints may be extracted
as well, thanks to module Cstr access functions (id, name,
fprint).
Early Backtrack
With FaCiLe as in Prolog systems, any dynamic modification
performed within goals may be undone (backtracked) to restore the
state of the system. However, no choice-point is associated to the
``root'' of the constraint program, so that variables modifications
occurring before the call to Goals.solve can never be
undone. As the standard way of adding constraints with FaCiLe is to
post them prior to the solving, i.e. statically outside goals, the
domain reductions initially made by these constraints are not
backtrackable.
2.6 Optimization
Classic Branch & Bound search is provided by the function
minimize of module Goals. It allows to solve a specified
goal (g) while minimizing a cost defined by a finite domain
variable (c):
-
Goal g is solved and the cost must then be bound to a value cc, i.e.
the current cost of the current solution
- Backtracking is performed to restore the state of the system as before the
execution of g and a new constraint stating c < cc is added to
the constraint store
- The process loops until goal fails
The third argument of Goals.minimize is a function
solution : int -> unit called each time a solution is found.
The argument of solution is the current value of the cost cc which must be instantiated by g. This function is
handy to store the last solution and cost in references, because
Goals.minimize always fails, so that the decision and cost
variables are restored as before its execution by Goals.solve.
The following example solves the minimization of x2+y2 while x+y=10:
let x = Fd.interval 0 10 and y = Fd.interval 0 10 in
Cstr.post (fd2e x + fd2e y = i2e 10);
let c = Arith.e2fd (fd2e x ** 2 + fd2e y ** 2) in
let store = ref None in
let solution cc =
store := Some (cc, Fd.elt_value x, Fd.elt_value y);
Printf.printf "Found let g = Goals.minimize (Goals.indomain x Goals.indomain y) c solution in
if Goals.solve (g || Goals.success) then
match !store with
None -> Printf.printf "No solution
n"
| Some (best_c, best_x, best_y) ->
Printf.printf "Optimal solution: cost= Found 100
Found 82
Found 68
Found 58
Found 52
Found 50
Optimal solution: cost=50 x=5 y=5
- : unit = ()
Additionally, Goals.minimize has two optional arguments:
-
?step: the improvement between two consecutive solutions must be
greater than step, i.e. the constraint posted each time a solution is
found is c £ cc - step; step default value
is obviously 1.
?mode: may be either Goals.Restart or Goals.Continue
(of type bb_mode);
with mode Restart, the search restarts from the beginning at
each step, i.e. the system backtracks until the very state prior to the execution of
minimize, whereas with mode Continue the search simply carries on
with an update of the cost constraint. Default mode is Goals.Continue.
2.7 Constraint Programs on Finite Sets
CP can be parameterized by the mathematical structure on which to
express variables and constraints. In (almost) the same way, FaCiLe
uses the generic mechanism of functors to provide variables
either on integers domain or on finite sets (of integers)
domain. Hence, the interface (of type BASICFD,
see ??) on which variables are built is the
same for both types (and then further extended for integer ones), once
parameterized by the Domain module, and once by
the SetDomain one.
So the few previous sections are relevant to document set variables
and constraints. Specific issues are discussed below.
2.7.1 Set Domains
The standard Domain module builds domain (of type
Domain.t) from its basic elements, integers, whose type is
aliased as Domain.elt. Similarly, the SetDomain module
builds domain of type SetDomain.t from basic elements, set of
integers with type SetDomain.elt. The latter type simply is
an alias for type SetDomain.S.t of module SetDomain.S
which provides values and functions to build and handle elements
of SetDomain (see ??).
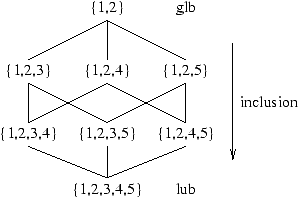
Set domains represent sets of integers
sets. They are described as powerset lattices of sets bounded by its
definite elements, the glb (Greater Lower Bound) and possible
elements lub (Lower Upper Bound). So the glb corresponds to the
min value of an integer domain while the lub corresponds to its
max.
Figure 2.1 illustrates the representation of the
following domain :
let glb = SetDomain.elt_of_list [1;2];;
val glb : Facile.SetDomain.elt = <abstr>
let lub = SetDomain.elt_of_list [1;2;3;4;5];;
val lub : Facile.SetDomain.elt = <abstr>
let sd = SetDomain.interval glb lub;;
val sd : Facile.SetDomain.t = <abstr>
SetDomain.fprint stdout sd;;
1 2 .. 1 2 3 4 5 - : unit = ()
Note that the glb must be included in the lub, and that "holes"
cannot be represented at the domain level.
Figure 2.1: Lattice of a set domain
2.7.2 Set Variables
The module defining set variables, SetFd, shares its interface
with module of integer variables Fd:
let sv = Var.SetFd.interval name:"sv" glb lub;;
val sv : Facile.Var.SetFd.t = <abstr>
Var.SetFd.fprint stdout sv;;
sv 1 2 .. 1 2 3 4 5 - : unit = ()
Var.SetFd.unify sv (SetDomain.S.empty);;
Exception: Fcl_stak.Fail "Var.XxxFd.subst".
However, specific (convenient) set operations (and constraints) are
located in module Conjunto:
Conjunto.inside 5 sv;;
- : unit = ()
Var.SetFd.fprint stdout sv;;
sv 1 2 5 .. 1 2 3 4 5 - : unit = ()
2.7.3 Constraints
Constraints on set variables can be found in module Conjunto
(see ??). Set operators like union, intersection,
subset... are provided, as well as operators involving integer variables
like cardinality or membership. The following example defines a fixed
set super and its 2-partition as sets sub1 and sub2.
It uses the union, disjoint and cardinal constraints of
module Conjunto:
let lub = SetDomain.elt_of_list [1;2];;
val lub : Facile.SetDomain.elt = <abstr>
let super = Var.SetFd.interval lub lub;;
val super : Facile.Var.SetFd.t = <abstr>
let sub1 = Var.SetFd.interval SetDomain.S.empty lub
and sub2 = Var.SetFd.interval SetDomain.S.empty lub;;
val sub1 : Facile.Var.SetFd.t = <abstr>
val sub2 : Facile.Var.SetFd.t = <abstr>
let card = Conjunto.cardinal (Conjunto.union sub1 sub2);;
val card : Facile.Var.Fd.t = <abstr>
Cstr.post (Conjunto.disjoint sub1 sub2);;
- : unit = ()
Cstr.post (fd2e card = i2e (SetDomain.S.cardinal lub));;
- : unit = ()
A specific goal is provided within module Goals.Conjunto
to non-deterministically instantiate set variables. The following
example enumerates and prints the 2-partitions of set super:
let print () =
Printf.printf "sub1=let g =
Goals.Conjunto.indomain sub1 Goals.Conjunto.indomain sub2
Goals.atomic print Goals.fail in
ignore (Goals.solve g);;
sub1= sub2= 1 2
sub1= 2 sub2= 1
sub1= 1 sub2= 2
sub1= 1 2 sub2=
- : unit = ()
- 1
- Type Var.concrete_fd constructors Unk and Val
stand respectively for ``Unknown'' (unbound) and ``Value'' (bound).
- 2
- Comparison functions return 0 if both arguments
are equal, a positive integer if the first is greater than the second
and a negative one otherwise (as specified in the OCaml standard
library).
- 3
- Not infix.